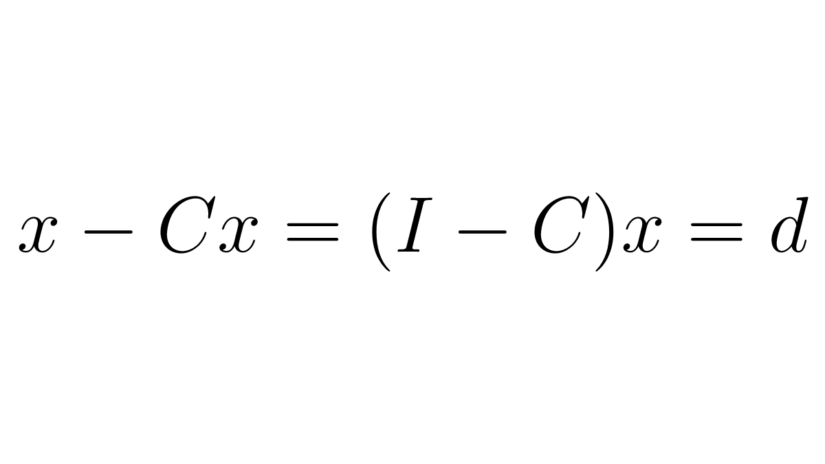The Leontif Input-Output Model
An input–output model are used in economics to model the inter-dependencies between different sectors of an economy. Wassily Leontief (1906–1999) is credited with developing the type of analysis that we explore in this chapter. His work on this model earned a Nobel Prize in Economics.
The input-output model assumes that there are sectors in an economy that produce a set of desired products to meet an external demand. The model also assumes that the sectors themselves will also demand a portion of the output that the sectors produce. If the sectors produce exactly the number of units to meet the external demand, then we have the equation $$(\text{sector output}) – (\text{internal consumption}) = (\text{external demand})$$ In this section we will see that this equation is a linear system that can be solved to determine the output the economy needs to produce to meet the external demand.
Example 1: The Internal Consumption Matrix
Suppose an economy that has two sectors: manufacturing (M) and energy (E). Both of the sectors produce an output to meet an external demand (D) for their products. Sectors M and E also require output from each other to produce output. The way in which they do so is described in the diagram below.
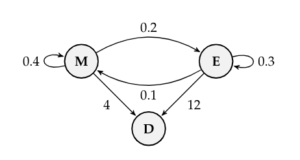
The numbers in the above diagram can be interpreted as follows.
- For every 100 units that sector M creates, M requires 40 units from M and 10 units from E.
- For every 100 units that sector E creates, E requires 20 units from M and 30 units from E.
- There is an external demand (D) requiring 4 units from M and 12 units from E.
In other words, if M were to create $x_M$ units, then M would consume $0.4x_M$ units from M and $0.1x_M$ units from E. To allow us to use the tools of linear algebra to approach this problem, we represent this consumption with a vector. The consumption from sector M could be represented in this way
$$\text{consumption from M} = \begin{pmatrix} 0.4x_M\\ 0.1x_M \end{pmatrix} = \frac{x_M}{10}\begin{pmatrix} 4\\1 \end{pmatrix}$$
Likewise, the consumption from sector E would be
\begin{align*}\text{consumption from E} &= \frac{x_E}{10} \begin{pmatrix} 2\\3 \end{pmatrix}\end{align*}
Adding these vectors together gives us the total internal consumption from both sectors.
\begin{align*}
\text{total internal consumption} &=
\frac{x_M}{10}\begin{pmatrix} 4\\1 \end{pmatrix} +
\frac{x_E}{10} \begin{pmatrix} 2\\3 \end{pmatrix} \\
&= \frac{1}{10} \begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix}\begin{pmatrix} x_M \\ x_E \end{pmatrix} \\
&= C \vec x, \quad \text{where } \ C = \frac{1}{10}\begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix}, \quad \vec x = \begin{pmatrix} x_M \\ x_E \end{pmatrix}
\end{align*}
Matrix $C$ is called the consumption matrix. Typically its entries are between 0 and 1, and the sum of the entries in each column of $C$ will be less than 1. Vector $\vec x$ is the output of the sectors. If the sectors produce exactly the number of units to meet the external demand, then we have the equation
\begin{align}
(\text{sector output}) – (\text{internal consumption}) & = (\text{external demand}) \\ \vec x – C\vec x & = \vec d
\end{align}
In our example, vector $\vec d = \begin{pmatrix} 4 \\ 12 \end{pmatrix}$, and $\vec x – C\vec x = (I – C)\vec x$. This simplifies the above equation to
\begin{align}
(I-C)\vec x & = \vec d \\
\left( \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} – \frac{1}{10}\begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix} \right)\begin{pmatrix} x_M \\x_E \end{pmatrix} & = \begin{pmatrix} 4\\12 \end{pmatrix} \\
\begin{pmatrix} 0.6 & -0.2 \\ -0.1 & 0.7 \end{pmatrix} \begin{pmatrix} x_M \\x_E \end{pmatrix} &= \begin{pmatrix} 4\\12 \end{pmatrix}
\end{align}
This is a linear system with two equations, whose solution gives us the output vector that balances production with demand. Expressing the system as an augmented matrix and using row operations yields the solution as shown below.
$$\left(\begin{array}{cc|c} .6&-.2&4\\-0.1&0.7&12 \end{array}\right) \thicksim \left(\begin{array}{cc|c} -1&7&120 \\ 6&-2&40 \end{array}\right) \thicksim \left(\begin{array}{cc|c} -1&7&120 \\ 0&40& 760 \end{array}\right) \thicksim \left(\begin{array}{cc|c} 1&0&13 \\ 0&1& 19 \end{array}\right)$$
The unique solution to this linear system is $\vec x = \begin{pmatrix} 13\\19 \end{pmatrix}$. This is the output that sectors M and E would need to produce to meet the external demand exactly.
Example 2: An Economy with Three Sectors
Suppose an economy that has three sectors: X, Y, and Z. Each of these sectors produce an output to meet an external demand (D) for their products. The way in which they do so is described in the diagram below.
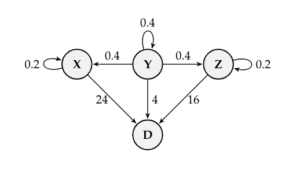
The external demand, D, is requiring 24 units from X, 4 units from Y, and 16 units from Z. Our goal is to determine how many units the sectors need to produce in order to satisfy this demand, while also accounting for internal consumption.
If Sector X were to create $x_X$ units, then it would consume $0.2x_X$ units from X and $0.4x_X$ units from Y. This consumption could be represented by the vector
$$\text{consumption from Sector X} = \begin{pmatrix} 0.2x_X\\ 0.4x_X\\ 0 x_X \end{pmatrix} = \frac{x_M}{10}\begin{pmatrix} 2\\4\\ 0 \end{pmatrix}$$
Likewise, the consumption from the other two sectors are
\begin{align*}
\text{consumption from Sector Y} &= \frac{x_Y}{10}\begin{pmatrix} 0\\4\\0 \end{pmatrix} \\
\text{consumption from Sector Z} &= \frac{x_Z}{10}\begin{pmatrix} 0\\4\\2 \end{pmatrix}
\end{align*}
Adding these three vectors together gives us the total internal consumption from all sectors.
\begin{align*}
\text{total internal consumption}
&=
\frac{x_X}{10}\begin{pmatrix} 2\\4\\0 \end{pmatrix} +
\frac{x_Y}{10}\begin{pmatrix} 0\\4\\0 \end{pmatrix} +
\frac{x_Z}{10}\begin{pmatrix} 0\\4\\2 \end{pmatrix} \\
&= \frac{1}{10} \begin{pmatrix} 2 & 0 & 0 \\ 4 & 4 & 4 \\ 0 & 0 & 2 \end{pmatrix}\begin{pmatrix} x_X \\x_Y \\ x_Z \end{pmatrix} \\
&= C \vec x, \quad \text{where } \quad C = \frac{1}{10}\begin{pmatrix} 2 & 0 & 0 \\ 4 & 4 & 4 \\ 0 & 0 & 2 \end{pmatrix}, \quad \vec x = \begin{pmatrix} x_M \\ x_A \\ x_E \end{pmatrix}
\end{align*}
$C$ is our consumption matrix. Each of the sectors in our economy are producing units to satisfy an external demand. The difference between the output and the internal consumption will represent the number of units produced to meet external demand.
\begin{align*}\text{remaining units to meed demand} &= (\text{sector output}) – (\text{internal consumption}) \\ &=\vec x – C\vec x \\ &= (I – C)\vec x \end{align*}
If the sectors are to meet the needs of the external demand exactly, the demand would need to equal the number of units produced after internal consumption is taken into account. That is, we need that
\begin{align*} (I – C)\vec x &= \vec d \end{align*}
This is a linear system that can be solved for the output vector, $\vec x$. This could be computed using an augmented matrix.
\begin{align*}\left(\begin{array}{c|c} I-C & \vec d \end{array}\right) &= \left(\begin{array}{ccc|c}
0.8 & 0 & 0 & 24\\ -0.4 & 0.6 & -0.4 & 4\\ 0 & 0 & 0.8 & 16
\end{array}\right) \\ &\thicksim \left(\begin{array}{ccc|c}
8 & 0 & 0 & 240\\ -4 & 6 & -4 & 40\\ 0 & 0 & 8 & 160
\end{array}\right) \\ &\thicksim \left(\begin{array}{ccc|c}
1 & 0 & 0 & 30\\ -4 & 6 & -4 & 40 \\ 0 & 0 & 1 & 20
\end{array}\right) \\ &\thicksim \left(\begin{array}{ccc|c}
1 & 0 & 0 & 30\\ 0 & 1 & 0 & 40 \\ 0 & 0 & 1 & 20
\end{array}\right)
\end{align*}
A helpful trick when reducing these matrices by hand is to multiply each row by 10 to make the algebra a bit less tedious. The above augmented matrix is in row reduced echelon form, and indicates that the desired output is
$$\vec x = \begin{pmatrix} 30\\40\\20 \end{pmatrix}$$