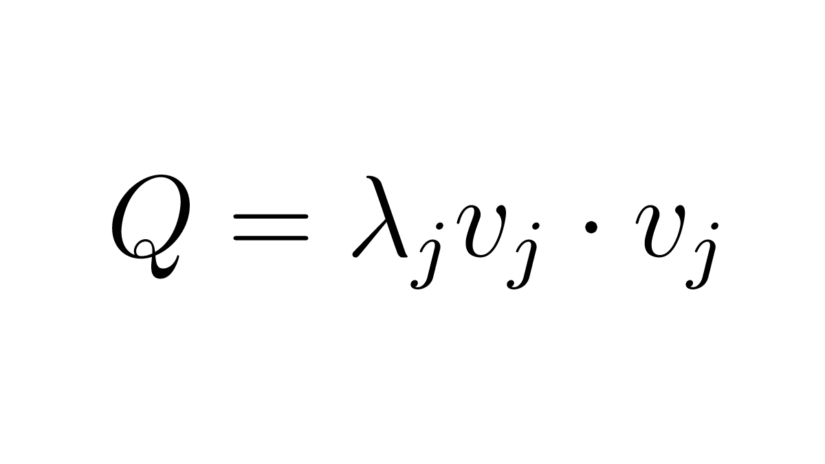Eigenvalues of Real Symmetric Matrices

The eigenvalues of a square matrix with real entries can be complex. For example, a quick calculuation will verify that the eigenvalues of

$$A = \begin{pmatrix} 1&-2\\2&1\end{pmatrix}$$

are $1\pm2i$. But when the matrix is symmetric, the eigenvalues must be real. In this post we give the proof that when $A=A^T$ and the entries of $A$ are real that the eigenvalues of $A$ must also be real.

The Complex Conjugate

To show that $Q$ is real, we will make use of the complex conjugate. We use the overbar notation to denote complex conjugate, so if $a$ and $b$ are real, then the complex number $z = a + i b$ has complex conjugate $\overline{z} = a – ib$. Moreover, if $\overline{z} = z$, then $b=0$ which implies that $z$ must be a real number. We use this idea in the next section to show that a quantity we need is real.

The Quadratic Form $Q=\bar x ^T A x$

First we will show that when $A$ is a real symmetric matrix that for any $x \in \mathbb C^n$ that the quantity $Q=\bar x ^T A x$ is real. Our approach will be to show that $\overline Q = Q$.
\begin{align*}
\overline Q = \overline{(\overline x^T Ax)} = \overline{\overline x} \, ^T \, \overline{Ax} = x^T \, \overline{Ax} = x^T A\overline x
\end{align*}
Next we apply the assumption that $A$ is real, so that $\overline A = A$. But $\overline Q$ is a number, so $\overline Q^T=\overline Q$ and
\begin{align*}
\overline Q = (\overline Q)^T = (x^T A\overline x )^T = \overline x^T (x^TA)^T =Q
\end{align*}
Because $\overline{Q}=Q$, we have shown that $Q=\overline x^T Ax$ is real for any $x \in \mathbb C^n$ and real symmetric $n\times n$ matrix $A$.

Eigenvectors of $A$

Next we use this result to show that when $x=v_j$ is an eigenvector of $A$ that $Q$ is equal to an eigenvalue of $A$.
$$Q = \overline x \, ^T Ax = \overline v_j \, ^T A v_j = \overline v_j \, ^T (\lambda_j v_j) = \lambda_j v_j \cdot v_j$$
But $v_j \cdot v_j$ is real and $Q$ is real, so $\lambda_j$ must also be real.